竹杖芒鞋轻胜马
谁怕?
一蓑烟雨任平生
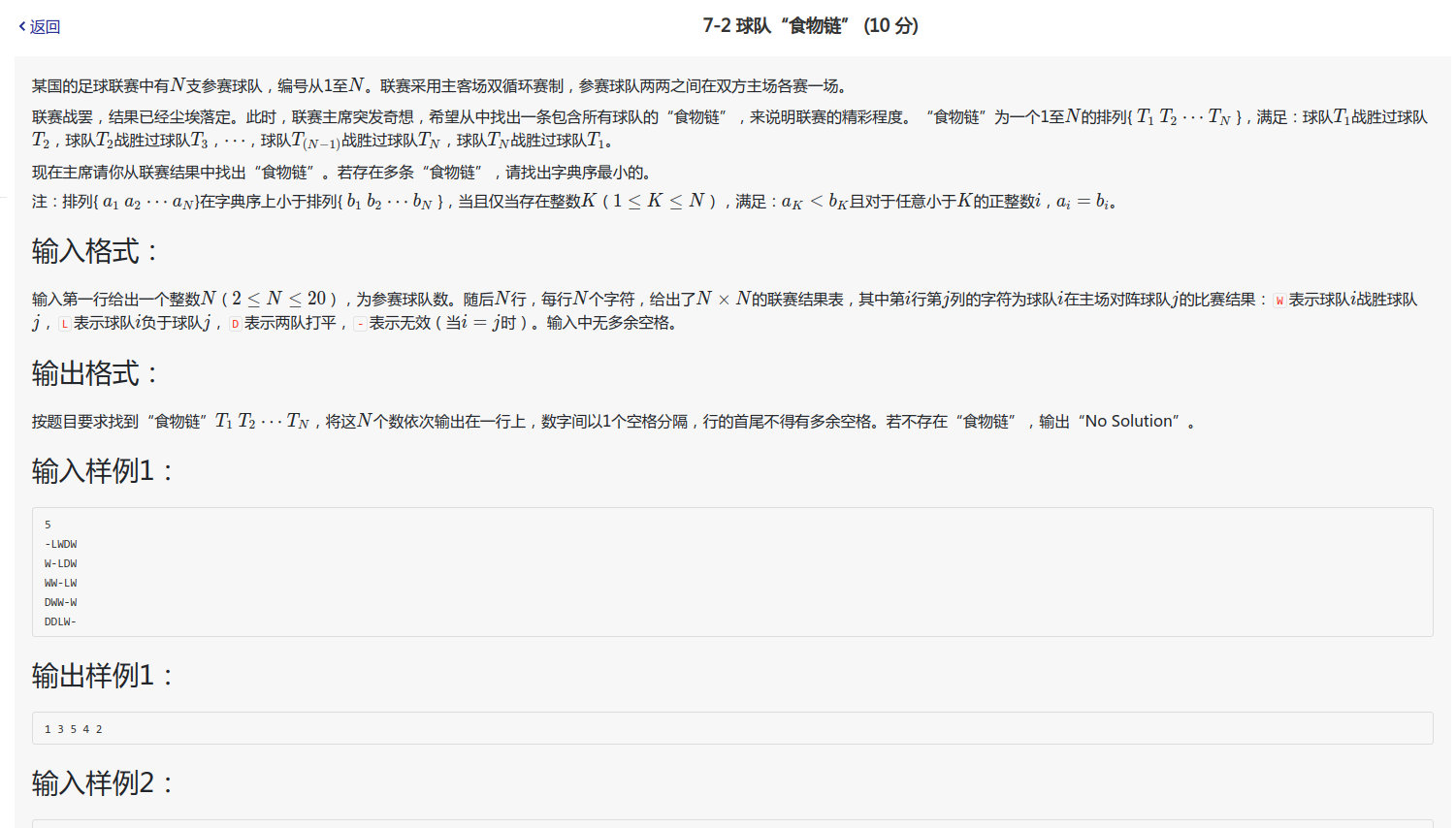
这是PTA上一道作业题,大概就是在有向图中找出一个字典序最小的环,要求这个环连接了所有的点。
首先想到的就是DFS了,思路如下:
- 根据输入,建立所有的有向边,当然可能出现双向的
- 使用深度优先遍历,用一个vector记录路径,用一个vis数组记录当前路径经过的点
- 每进入下一个点前,判断这个点有没有访问过,是不是连通
- 如果记录路径的vector存下了n个点,说明已经存下了所有点了,然后看首尾相等吗
- 首尾相等则说明找到答案了,我们是按照从小到大找的,所以不用考虑字典序
看上去没大问题了,写下来,一交,超时了。
想了好多可能超时的点,都觉得不科学,按理说已经不能降低复杂度了。
只能搜一下了,看了下博客上别人的题解,才意识到问题没那么简单。
这个题目有几个信息必须抓住:
- 环上包括了所有的点
- 字典序最小,则意味着环要有个头的话,一定是1!
- 第三点最重要:如果剩下的点中没有能和1相连通的,就不用遍历了,因为没有能够连接头的了,成不了环
有了以上分析,就可以下写出下面的代码了:
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
int g[21][21];
int n;
vector<int> ans;
bool vis[21];
void dfs(int root, vector<int> &tpath, bool &flag) {
if (flag) return ;
if (tpath.size() == n && g[root][1] == 1) {
ans = tpath;
flag = true;
}
bool cango = false;
for (int i = 1; i <= n; i++) {
if (!vis[i] && g[i][1] == 1)
cango = true;
}
if (!cango) return ;
for (int next = 1; next <= n; next++) {
if (!vis[next]) {
if (g[root][next] == 1) {
vis[next] = true;
tpath.push_back(next);
dfs(next, tpath, flag);
tpath.pop_back();
vis[next] = false;
}
}
}
}
int main() {
cin >> n;
getchar();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
char ret;
scanf("%c", &ret);
if (ret == '-') g[i][j] = 0;
else if (ret == 'W') g[i][j] = 1;
else if (ret == 'L') g[j][i] = 1;
}
getchar();
}
vector<int> tpath;
bool flag = false;
for (int i = 1; i <= n; i++) {
vis[i] = true;
tpath.push_back(i);
dfs(i, tpath, flag);
tpath.pop_back();
vis[i] = false;
}
if (flag) {
for (int i = 0; i < n; i++) {
if (i != n - 1)
printf("%d ", ans[i]);
else
printf("%d", ans[i]);
}
} else printf("No Solution");
return 0;
}