C++ 实现 Pratt Parsing

连雨不知春去

一晴方觉夏深

写作本文一方面是为了巩固笔者所学，另一方面也是将自己的一些理解分享给有缘的读者，希望能帮助到大家。本文在写作之前受到了文章手写一个Parser - 代码简单而功能强大的Pratt Parsing 的启发，该文章对 Pratt Parsing 的描述十分细致，由浅入深，感谢大佬！

Pratt Parsing

在跟Crafting Interpreters的时候，看到clox解析表达式 compiling-expressions的时候用了这种Parsing。初次接触，这一节我看了很久，虽然跟着作者的代码和文字写出来了，也能顺利生成字节码。但我清楚地明白自己并没有搞懂这是怎么来的，Prefix和Infix到底代表了什么，为什么通过 parsePrecedence() 就能把结合性（associativity）和优先级（Precedence）就都处理好了，再加上递归，确实有一定的理解难度。后来为了彻底搞明白，在跟这部分内容的时候，我实现的 Parser 做了一定的改动，不是直接输出字节码，而是先生成AST（抽象语法树），同时把Parser独立出来了，作者实现的Parser是直接和Compile塞一起的。因为自己菜，实现用的是C++，而不是纯C，命名为cclox。于我个人而言，C相对缺乏抽象，写编译器/解释器不如C++来的直观，特别是后面实现Object/String的时候。

ASTRef Parser::ParsePrecedence(Precedence precedence) {
    Advance();

    const PrefixParseFn & prefixRule = GetRule(_previousToken._type)->_prefixFn;
    if (prefixRule == nullptr)
    {
        ErrorAt(_previousToken, "Expect expression.");
        return nullptr;
    }

    ASTRef left = prefixRule();

    while (precedence <= GetRule(_currentToken._type)->_precedence) {
        Advance();
        InfixParseFn infixRule = GetRule(_previousToken._type)->_infixFn;
        left = infixRule(std::move(left));
    }
    return left;
}

是什么

Pratt Parsing，是由作者 Vaughan Pratt 在1973年发表的 Top down operator precedence 中提出，是一种擅长解析表达式的算法。Pratt Parsing 也是基于递归下降算法，但相对于 recursive descent，Pratt Parsing 能够很好的处理优先级（precedence）和结合性（associativity）。

举个很简单的例子，对于于以下的表达式：

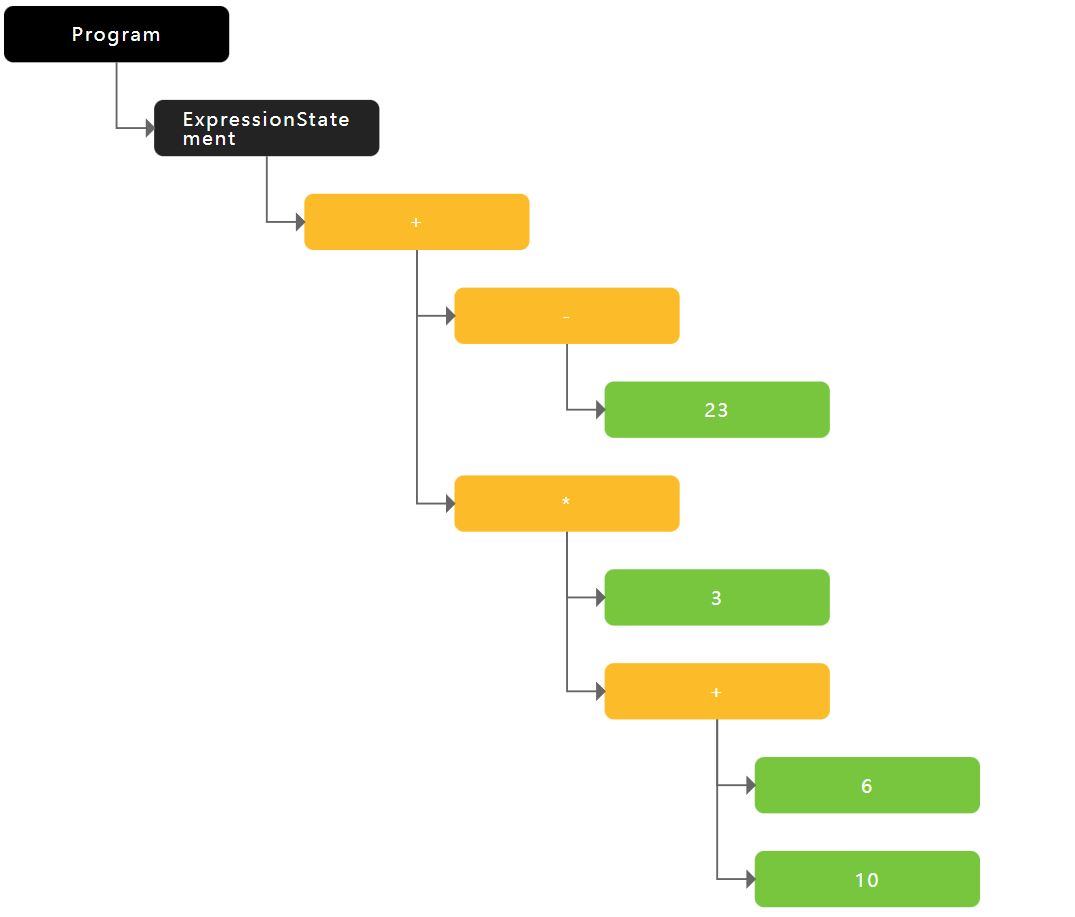
-23 + 3 * (6 + 10)

我们很容易就能将其按照优先级理解成以下结构：

(-23) + (3 * (6 + 10))

从AST的角度理解，可以画出如下二叉树：

如果用 Pratt Parsing 的角度理解呢？

expr:                        -      23      +      3      *      6      +      10
power:                          8      6.1     6     7.1    7       9      9

如上，Pratt Parsing会按照 Precedence 和 Associativity 按以上规则解析，不过还不直观，接下来通过相关概念和算法流程来一一剖开 expr 和 precedence 的秘密。

Precedence 优先级

算术符优先级大家在入门的时候都学过，直接通过枚举，可以定义各个运算符和 Token 的优先级如下：

typedef enum {
    PREC_NONE,        // Declaration, Definition, Number, String, Literal...
    PREC_ASSIGNMENT,  // =
    PREC_OR,          // or
    PREC_AND,         // and
    PREC_EQUALITY,    // == !=
    PREC_COMPARISON,  // < > <= >=
    PREC_TERM,        // + -
    PREC_FACTOR,      // * /
    PREC_UNARY,       // ! -
    PREC_CALL,        // . ()
    PREC_PRIMARY
} Precedence;

大部分都很容易理解，其中 Declaration, Definition, Number, String, Literal…其实不能算是运算符，其优先级为 None，最终这些符号都会被 “贴附” 在对应的运算符上，组成其他 Token 的 “子表达式”。

Prefix & Infix

要真正理解Pratt Parsing，Prefix 和 Infix 非常重要，包括 Token 和 Function。

prefix token: 以当前 Token 为最低优先级的子表达式中（以下用“子表达式”指代），该 Token 必然位于最左端
- Unary: “-“
- Group: “(“
- Number
- String
- …
prefix function: 用于生成 prefix token 对应的子表达式的function
infix token: 以当前 Token 为最低优先级的子表达式中，该 Token 必然不位于两端
- ”+”
- ”-“
- “*”
- ”/”
infix function: 用于生成 infix token 对应的子表达式的function

对于Group “()”的处理，我们先按下不表。”以当前 Token 为最低优先级的子表达式中”，这句话是理解 Pratt Parsing 的核心。其中优先级为 None 的 Token 将贴附在其他 Token 的子表达上，也就是 AST 的叶子节点，以本文上述表达式为例：

-23 + 3 * (6 + 10)

很显然，”23”的子表达式就是”23”，负号 “-“ 的子表达式就是 “-23”。以此类推，乘号 “*” 的子表达式就是 “3 * (6 + 10)”，可以手动列出下结果：

负号 “-“ ，Prefix Token，子表达式：”23”
第二个加号 “+” Infix Token，子表达式：”6 + 10”
乘号 “*” Infix Token，子表达式：3 * (6 + 10)
第一个加号 “+” Infix Token，子表达式：”(-23) + (3 * (6 + 10))”

而Prefix Function 和 Infix Function就是用于解析出这些子表达式的所在，这也是为什么 Prefix Token 在对应的子表达式中一定位于最左端。建议根据以上几个例子，理解 “以当前 Token 为最低优先级的子表达式” 后，再阅读下文。

Parse Precedence

Parse Precedence一般被认为是Pratt Parsing的核心部分，以下是我在cclox中实现的代码：

ASTUniquePtr Parser::ParsePrecedence(Precedence precedence) {
    Advance();

    const PrefixParseFn & prefixRule = GetRule(_previousToken._type)->_prefixFn;
    if (prefixRule == nullptr)
    {
        ErrorAt(_previousToken, "Expect expression.");
        return nullptr;
    }

    ASTUniquePtr left = prefixRule();

    while (precedence <= GetRule(_currentToken._type)->_precedence) {
        Advance();
        InfixParseFn infixRule = GetRule(_previousToken._type)->_infixFn;
        left = infixRule(std::move(left));
    }
    return left;
}

在理解 ParsePrecedence() 之前，首先要明白其输入输出是什么：

输入：某个 Precedence 级别 precedence
输出：从下一个 Token 开始，最低优先级（None除外，特别注意：Group “()” 会重置优先级）高于 precedence 的子表达式或者AST

仍然以上文表达式为例：

-23 + 3 * (6 + 10)

如果输入为 PREC_FACTOR，对应的 Token 为 “*“，那么得到的子表达式为 “6 + 10”
如果输入为 PREC_TERM，对应的 Token 为第一个 “+”，那么得到的子表达式为 “3 * (6 + 10)”
如果输入为 PREC_TERM，对应的 Token 为第二个 “+”，那么得到的子表达式为 “10”
… 以此类推

所以能明白 ParsePrecedence() 的作用就是：遍历后续的 Token 流，得到一个新的子表达式，要求该子表达式中运算符的 Token 的最低优先级不能低于输入的 precedence，优先级为 None 的 Token 不需要考虑，因为这些 Token 会被其他 Token 吸附为子表达式。特殊情况：如果有Group “()” 存在，输入的 precedence会被重置为 Assignment 赋值的优先级，后续会详细分析。

我们一步步理解上述代码：

ASTUniquePtr Parser::ParsePrecedence(Precedence precedence) {
    Advance();

    ...

Advance() 是从 Sacnner 中取出下一个 Token，可以得到我们要处理的 Token。

ASTUniquePtr Parser::ParsePrecedence(Precedence precedence) {
    ...

    const PrefixParseFn & prefixRule = GetRule(_previousToken._type)->_prefixFn;
    if (prefixRule == nullptr)
    {
        ErrorAt(_previousToken, "Expect expression.");
        return nullptr;
    }

    ASTUniquePtr left = prefixRule();

这里是根据新的 Token ，随后执行 Prefix Function，根据本文上述，这里会得到 Prefix Token 的子表达式，比如 Prefix Token 是负号 “-“ ，那么这里 prefixRule() 返回的就是子表达式 “-23”。

继续分析Infix的处理。

ASTUniquePtr Parser::ParsePrecedence(Precedence precedence) {
    ...

    while (precedence <= GetRule(_currentToken._type)->_precedence) {
        Advance();
        InfixParseFn infixRule = GetRule(_previousToken._type)->_infixFn;
        left = infixRule(std::move(left));
    }
    return left;
}

这个 while 循环里，将取出的 Token 的 Precedence 和输入的 precedence 进行比较，对于高于 precedence 的 Token，将执行其 Infix Function，这里注意会将 Prefix Function 得到的 left 表达式/AST一同传入。这是因为 Infix Function 构造 Infix Token 对应的子表达式，同时需要两侧的 Token。比如 Infix Token 是乘号 “*” ，则需要先有 left 表达式为 “3”，那么这里 infixRule() 返回的就是子表达式 “3 * (6 + 10)”，但是此处与前文说到的”子表达式”概念相悖。为什么 “+” 的优先级明显比 “*” 低，返回的还是 “6 + 10” 这样的子表达式呢？

在Pratt Parsing 处理 Group “()”的时候，这里子表达式 “6 + 10” 不是以 “*” 作为 precedence 输入，而是 “=”。

经过 Group “()” 以后，precedence 将被重置为 PREC_ASSIGNMENT：

ASTUniquePtr Parser::Group() {
    ASTUniquePtr groupedAst = Expression();
    Consume(TOKEN_RIGHT_PAREN, "Expect ')' after expression");
    return groupedAst;
}

ASTUniquePtr Parser::Expression() {
    return ParsePrecedence(PREC_ASSIGNMENT);
}

所以对于存在 Group “()” 的表达式，都需要经过优先级重置，Prefix也是同理。比如表达式：

-(2 + 30)

在处理 Prefix Token Unary “-“ 时，执行 Prefix Function，会通过执行 Group() 将 precedence 输入重置为 PREC_ASSIGNMENT。

我在cclox中实现的 Unary Prefix Function如下：

ASTUniquePtr Parser::Unary() {
    ASTUniquePtr unaryAst = std::make_unique<UnaryExprAst>(_previousToken);
    unaryAst->_rhs = ParsePrecedence(PREC_UNARY);
    return unaryAst;
}

以及 Binary Infix Function：

ASTUniquePtr Parser::Binary(ASTUniquePtr left) {
    auto binAst = std::make_unique<BinaryExprAst>(_previousToken);
    TokenType binOpType = _previousToken._type;
    ParseRule *rule = GetRule(binOpType);

    binAst->_lhs = std::move(left);
    binAst->_rhs = ParsePrecedence((Precedence)(rule->_precedence + 1));
    return binAst;
}

可以看到这两者都会递归调用 ParsePrecedence() 来继续得到自己的子表达式/AST，Infix Function 同时需要 left 作为AST的左子树。

测例分析

这时候再回头看之前的例子：

expr:                        -      23      +      3      *      6      +      10
power:                          8      6.1     6     7.1    7       9      9

可以根据递归顺序，分解为如下调用，首先作为表达式，最低优先级运算符是赋值，所以有 ParsePrecedence(PREC_ASSIGNMENT)：

ParsePrecedence(PREC_ASSIGNMENT = 1)

PrefixFunction(token = "-") -> “-23”
- ParsePrecedence(PREC_UNARY = 8) -> “23”
  - PrefixFunction(token = "23") -> “23”
InfixFunction(left = "-23", token = "+")
- ParsePrecedence(PREC_TERM = 6)
  - PrefixFunction(token = "3") -> “3”
  - InfixFunction(left = "3", token = "*")
    - ParsePrecedence(PREC_FACTOR = 7)
      - PrefixFunction(token = "(") -> “(6 + 10)”
        
        ParsePrecedence(PREC_ASSIGNMENT) -> “6 + 10”
        
        PrefixFunction("6") -> “6”
        
        InfixFunction(left = "6", token = "+") -> “6 + 10”
        
        ParsePrecedence(PREC_TERM = 6)”
        
        PrefixFunction("10") -> 10
        
        return -> “10”
        
        return -> “6 + 10”
        
        return -> “6 + 10”
      - return -> “(6 + 10)”
    - return -> “(6 + 10)”
  - return -> “3 * (6 + 10)”
- return -> “3 * (6 + 10)”
return -> “-23 + 3 * (6 + 10)”

有兴趣的读者也可以把我的 cclox仓库 clone下来，不依赖任何第三方库，可以看看是如何生成AST和输出字节码的，如果运行成功，会输出字节码：

总结

从实现来看，Pratt Parsing 的优势在于，处理每个 Token 或者子表达式时，不需要关注当前所处的表达式嵌套层级和全局状态。每个 Prefix Function 和 Infix Function，都仅关注如何构造对应 Token 的子表达式，最后通过递归得到更大的表达式/AST。结合 ParsePrecedence() ，Pratt Parsing 会在遍历 Token 的过程中，将每个 Token 放在合适的AST/表达式的结构里。由于上述特点，相对于递归下降算法，用 Pratt Parsing 处理表达式也就更得心应手。

Partt Parsing

Pratt Parsing

是什么

Precedence 优先级

Prefix & Infix

Parse Precedence

测例分析

总结

CATALOG

FEATURED TAGS

FRIENDS